RSA encryption is one of the most widely used encryption standards in use today and to solve this challenge we will need to understand how it works at a basic level.
RSA Crash Course
First let’s define some variables. The letters I’m choosing are somewhat standard in examples not just random.
- p + q : Two large prime numbers that multiplied together to get n. In order for RSA to work p and q must be secret.
- n : The result of p * q. n will serve as our modulus. This mathematical function is used for key generation, encryption, and decryption A modulus is a mathematical operation where you divide by one number and then take remainder as your result. For example, take an analog clock face. Let’s say we need to know what 13mod12 is. We would go around the clock till we got to 12 but then the clock would start over and we’d land on 1 our remainder. This how modulo works. This mathematical operation has no direct inverse function. Thus making it near impossible to crack.
- e : The public exponent. This is a relatively small prime number. It is chosen to be relatively prime to the value of (p – 1)*(q – 1).This Euler’s totient function for n. This will serve as part of our private key for encryption.
- Relatively prime : Two numbers are considered “relatively prime” (also known as “coprime” or “mutually prime”) if they share no common positive integer divisors other than 1. In other words, the greatest common divisor (GCD) of the two numbers is equal to 1. For example, 35 and 12. Neither of these numbers are prime but they share no common divisors other that 1.
- Euler”s Totient Function ϕ(n) : This function calculates the count of positive integers less than n that are relatively prime to n. In the context of RSA, This is the number of possible e values that will work securely with n.
- d : This is the private exponent that is used for decrypting. This number must also remain secret. It is chosen to satisfy this condition e⋅d≡1 (mod ϕ(n)). Don’t worry about understanding to math behind it. The main takeaway is that d is necessary for decrypting the cipher text and calculated using p, q, and e.
- m : This is our plain text message
- c: This is our cipher text aka our message when encrypted.
- Public key (n ,e)
- Private key (n, d)
Now Let’s walkthrough an example of how all of this is used.
- Alice has a message (m) that she wants to send to Bob but she has to encrypt it first. She takes Bob’s public key (n, e)and encrypts it generating a cipher text (c). The mathematical equation for this is c = m^emodn. The cipher text is raised to the power of the exponent then used in modulus operation with n
- Bob receives Alice’s message and decrypts it using the equation m=c^modn. This is nearly identical to our encryption equation except we are using the private key (n, d)

RSA encryption works because it is incredibly difficult to guess the values p and q from n, so long that n is long enough. In this challenge we are give the cipher text as well as the public key (n, e). The value of n is a little short for encryption so let’s use an online tool to factor p and q.
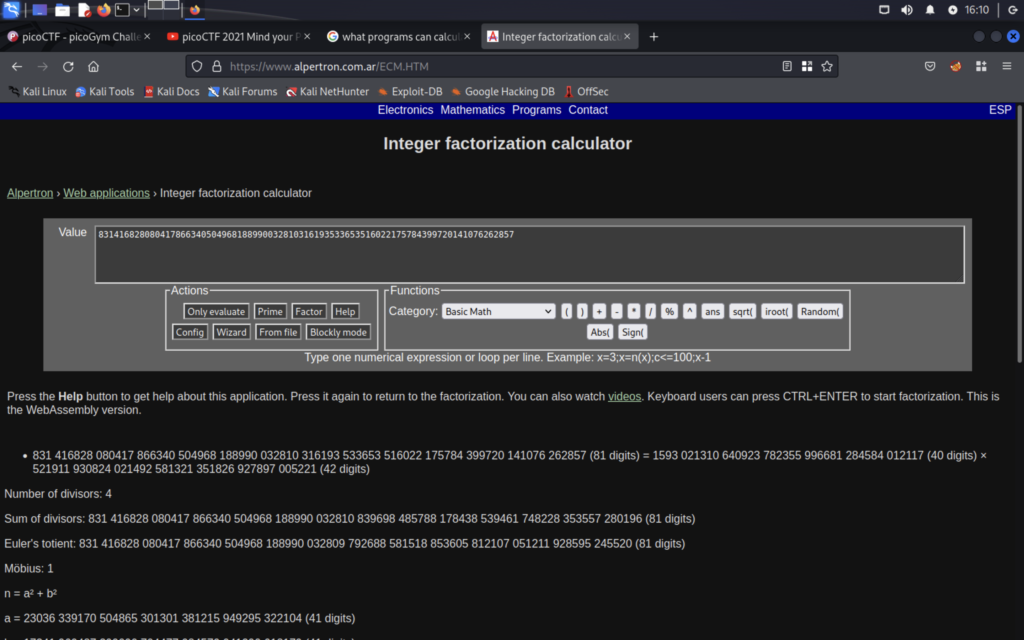
I used this site to factor our two values p and q. Now that we have those values we can use another tool to calculate d.
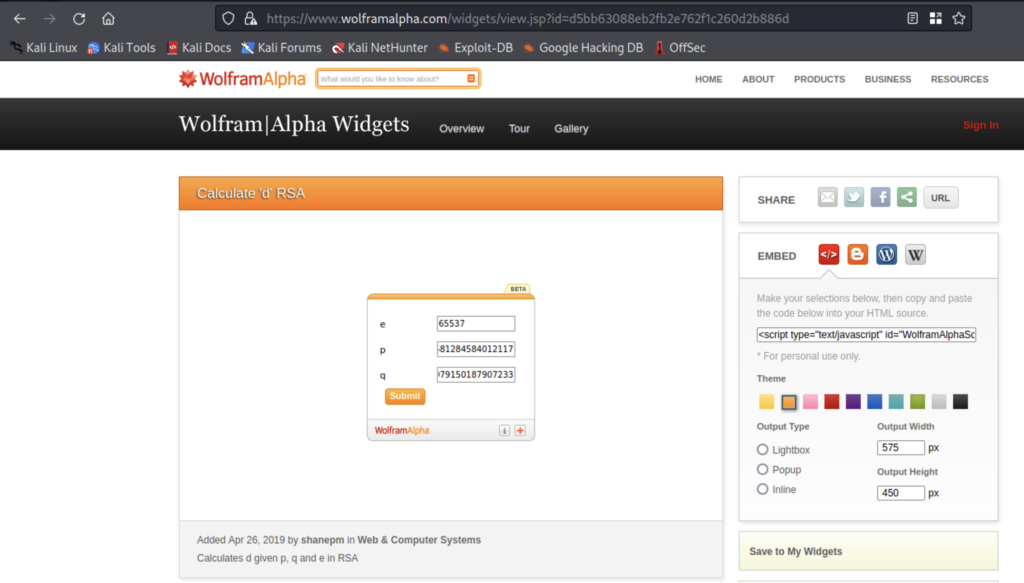
This website will calculate the value of d for us

Now we have all the tools necessary to decrypt c. We can do this using python
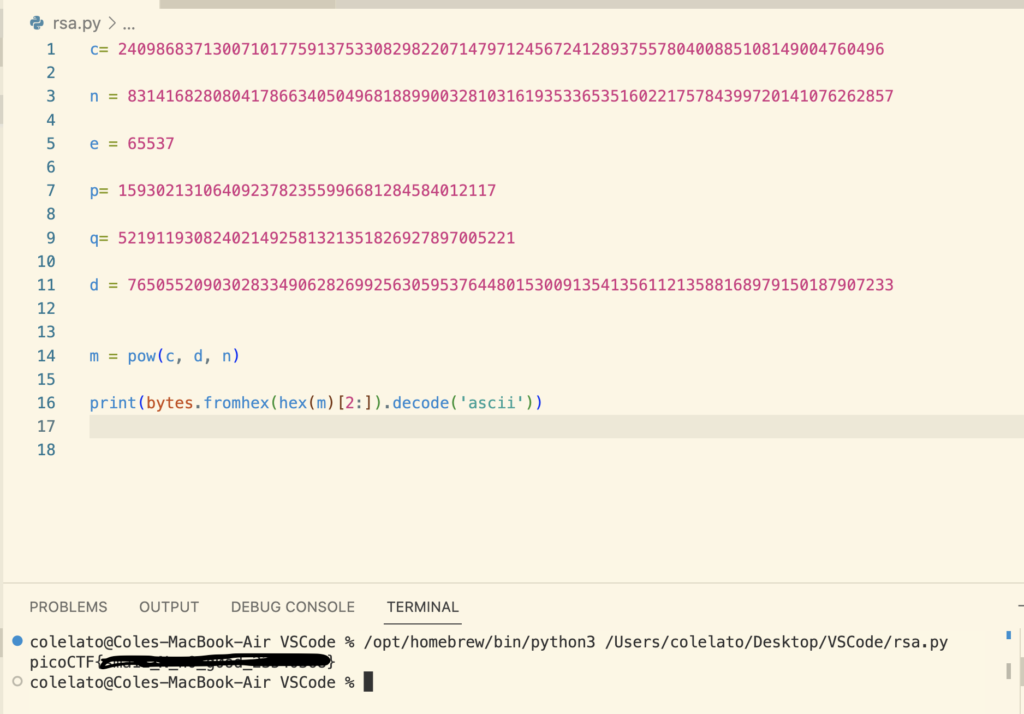
First I defined all of our variables; we wont need all of them. Then I used the pow() function to calculate m. The syntax is pow(base, exponent, modulus(optional)). We have already covered the equation for decryption so I’ll move on to the next line.
print(bytes.fromhex(hex(m)[2:]).decode(‘ascii’))
- First we use hex(m) to covert m to hexadecimal value
- When we create a hexadecimal value all numbers will have a”0x” at the front. The [2:] slices this value off.
- bytes.fromhex() converts our hex string back into bytes. The bytes represent the binary data of the hex string
- Then these values are decoded as ascii using .decode